La última entrada de nuestro blog nos permite conocer los conceptos básicos de la asimilación de datos en modelos numéricos y esta semana hemos elegido otro tema de la modelización meteorológica: esta vez hablaremos de algunos rasgos fundamentales de los modelos de área limitada. Definiremos cuáles son las características que distinguen estas herramientas de los modelos globales y abordaremos los aspectos que se deben tener en consideración a la hora de trabajar con ellos.
Los límites espaciales del modelo
Cuando hablamos del dominio de un modelo meteorológico, nos referimos al área de cobertura de él. Los modelos de área limitada (LAM) se ejecutan en un conjunto de cubos que disponen de lados tanto horizontales (laterales) como verticales (superiores e inferiores), mientras que los modelos globales que cubren toda la tierra, sólo tienen límites verticales. Uno de ellos es un contorno artificial: cada modelo trabaja con sus propios criterios para definir el límite superior de la atmósfera que incluso puede variar de una simulación a otra, efectuando los cambios a través de la función de la coordenada vertical. Normalmente a este superficie le corresponde una presión constante y muy baja (en la mayoría de los casos suele ser entre 5-50 hPa), definiendo una capa suficientemente ancha para cubrir todos los procesos atmosféricos que puedan afectar la predicción. El otro límite, el inferior está bien definido por la superficie de la Tierra, que no quiere decir que el tratamiento de este contorno sea una parte sencilla del sistema del modelo ya que la interacción entre la atmósfera y la superficie terrestre juega un papel fundamental prácticamente en todas las escalas meteorológicas.

La necesitad de la definición de los contornos para todos los modelos tiene su razón matemática: las ecuaciones hidrodinámicas sólo se pueden resolver utilizando métodos numéricos y los cálculos de cualquier tipo de estas aproximaciones comienzan con el “estado inicial” del sistema. A nivel de las coordenadas espaciales es equivalente al punto de partida, es decir el límite del dominio, mientras que la representación temporal de estas condiciones es el tiempo inicial de la simulación. La mayor diferencia entre los modelos globales y de área limitada consiste en la necesidad de definir las condiciones de contorno. Cabe mencionar que este único aspecto implica una serie de consecuencias que hay que tener en cuenta a la hora de trabajar con los LAM-s.
Primer paso: definición del dominio
A continuación nos enfocaremos en los modelos de área limitada, abordando primero algunas cuestiones fundamentales que están relacionadas con las características básicas del dominio de un modelo de área limitada.
- La proximidad del área de interés a los límites del modelo.
Los contornos se pueden considerar como un emisor potencial de los errores que se propagan hacia el interior de los límites durante la simulación. Dado que la influencia de los contornos es transportada por el campo de movimiento previsto, la propagación variará de un régimen a otro. Es muy habitual que los errores de una predicción sobre Europa Occidental sean más notables en la parte izquierda del dominio aunque el objetivo es disminuirlos de manera que no se manifiesten en las variables más importantes. De todas formas, para estimar la zona de mayor incertidumbre, debemos prestar atención al tiempo que tarda una trayectoria en desplazarse desde el límite del modelo hasta las proximidades de su zona de previsión.
- La resolución horizontal del modelo de mayor escala.
Las deficiencias en su pronóstico (sea cual sea la causa, una de ellos es la resolución inadecuada) influirán en el modelo de dominio menor y amplificarán los errores durante el período de la predicción. Entre los ejemplos más comunes figuran los errores en la posición, la intensidad y la estructura de los sistemas de baja presión, los frentes asociados, el chorro atmosférico, etc. En este aspecto es importante proporcionar datos en una resolución temporal adecuada que sea notablemente inferior al tiempo característico de dichos fenómenos.
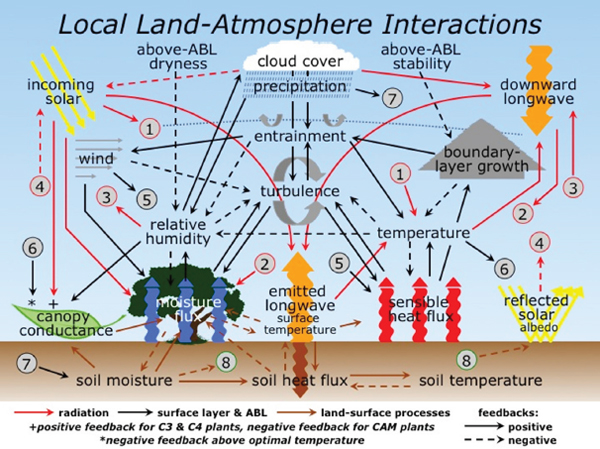
- Las condiciones inferiores, en particular la forma en que se prescriben y la exactitud de las parametrizaciones utilizadas para determinarlas.
La exactitud con que se describen los procesos físicos es crucial para el pronóstico de muchos elementos meteorológicos sensibles, como la temperatura, el perfil del viento, la turbulencia en la capa límite o la precipitación.
- Evaluación de los costes de cálculo.
El objetivo principal de ejecutar un modelo de área limitada suele ser obtener una predicción más exacta sobre un área concreta y sobre todo representar una gama más amplia de fenómenos meteorológicos. Como la escala de los procesos explícitamente resueltos por un modelo está altamente relacionada con la resolución horizontal, evidentemente queremos aumentar el número de puntos de la malla sobre la región de interés. Esto implica un aumento de cálculos de los que nuestro computador se tiene que enfrentar. Cuando preparamos un nuevo producto, uno de los primeros pasos es encontrar el equilibrio entre la estabilidad, fiabilidad y nuestra capacidad de cálculo.
El proceso clave: interacción entre las escalas distintas
Las condiciones de contorno sirven básicamente para proporcionar la única información sobre el estado atmosférico fuera del dominio. Por una parte, esto significa que un frente frío tiene que entrar por donde y cuando le toca pero por otra parte implica una consecuencia importante. Suelen decir que – sobre todo en dominios pequeños – las condiciones de contorno mandan sobre el modelo de menor escala después de un cierto tiempo de asimilación, por lo menos en cuanto a los fenómenos de escala mayor. Por ejemplo, para un dominio que abarca la mitad occidental del Mar Mediterráneo, las ondas largas atmosféricas están determinadas por la información que entra por los laterales y el modelo de área limitada las irá escalando hacia los procesos más pequeños. Concretamente, en el caso de los modelos mesoescalares de alta resolución podemos afirmar que los rasgos de escala sinóptica están determinados casi completamente por el modelo que proporciona las condiciones de contorno. De esa forma, las tareas están repartidas: el modelo exterior trae el frente frío y el modelo mesoescalar desarrolla las tormentas sobre él.
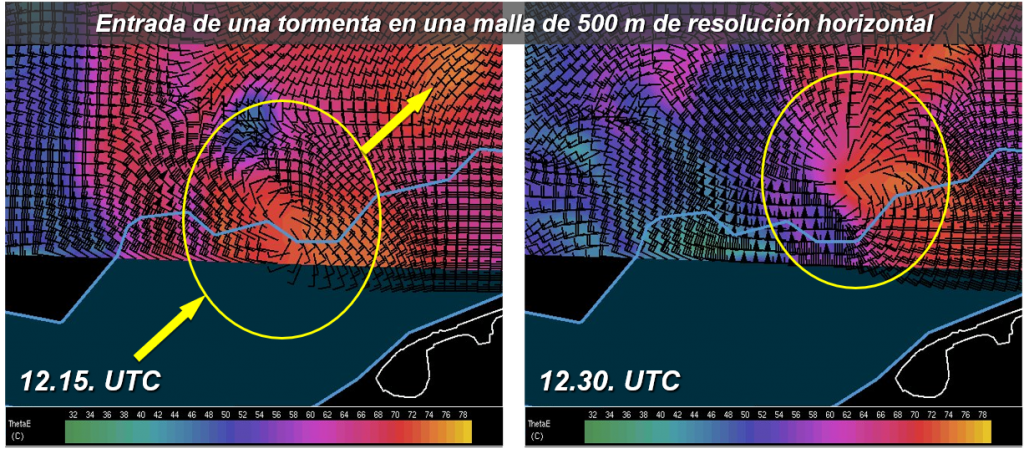
Como hemos visto anteriormente, a fin de resolver las ecuaciones de pronóstico se debe proporcionar información precisa de todas las variables de pronóstico en cada contorno. Los valores normalmente pueden obtenerse de diversas fuentes, entre ellas: como resultado de sistemas de asimilación de datos, predicciones anteriores de un modelo de mayor escala, algún tipo de valor climatológico o fijo (para especificar ciertas características de la superficie, como la temperatura de la superficie del mar, el tipo de vegetación, etc.).
Las condiciones de contorno normalmente suelen obtenerse de una ejecución anterior de un modelo de dominio mayor. Por ejemplo, un pronóstico de 6 a 54 horas de un modelo global ejecutado a las 18 UTC podría proporcionar las condiciones de límite lateral para un pronóstico de 0 a 48 horas de un modelo regional a partir de las 00 UTC. Se puede distinguir entre dos formas de interacción entre los resultados proporcionados por cada uno de los modelos. Si la información fluye en una dirección, desde el pronóstico previamente integrado sobre el dominio más grande al modelo de dominio más pequeño, hablamos de una interacción unidireccional.
Los modelos mesoescalares tienen implementados la posibilidad de realizar un zoom sobre una región predeterminada para trabajar en ella con mayor resolución. La necesidad surge debido a limitaciones computacionales, ya que el trabajo con grandes dominios de resolución elevada es muchas veces inviable. En la técnica llamada “one way nesting” se resuelve en primer lugar la física del dominio exterior y la información obtenida se transmite al dominio interior para resolver a continuación las ecuaciones de modelo en este dominio de mayor resolución. Utilizando esta técnica no se tiene en cuenta la retroalimentación al dominio padre que en caso de dominios múltiples reduce el coste de cálculo significativamente sin perjudicar la calidad de las predicciones. Los estudios y nuestras experiencias también confirman que el anidamiento unidireccional presenta un comportamiento más robusto y presenta menor sensibilidad a la localización de los límites laterales del dominio interno que bajo uso operacional es un aspecto primordial. Esta aproximación es análogo al concepto de la interacción unidireccional previamente mencionado. El “two way nesting” puede aumentar la veracidad de los resultados en casos de estudio concretos cuando se puede llevar a cabo varios experimentos con diferentes configuraciones para el mismo caso. En esta aproximación la retroalimentación es bidireccional que sólo es una forma viable cuando el control sobre el modelo exterior tenemos nosotros.
Fuentes de error
Finalmente, dedicamos unas frases a los fuentes de error más importantes que debemos disminuir en la medida que sea posible cuando ejecutamos una simulación con un LAM.
El primer grupo de errores está relacionado con la fiabilidad del pronóstico producido por el modelo que suministra las condiciones de contorno:
- Antigüedad de los datos de contorno.
- Representación de gradientes insuficiente en el modelo global.
Normalmente, las parametrizaciones físicas y las ecuaciones dinámicas de los dos modelos presentan grandes diferencias, lo que puede conducir a otro grupo de errores:
- Diferencias en la resolución vertical
- Diferencias de la representación del terreno en los contornos
- Diferentes parametrizaciones físicas.
Nuestro sistema basado en LAM
Meteoclim dispone de sus propias configuraciones del modelo WRF trabajando en varios dominios para generar sus predicciones a corto plazo y satisfacer las necesidades de sistemas acoplados como el WRF-Fire. Aunque es posible ejecutar el modelo en el globo entero, el WRF está diseñado principalmente para enfrentarse al desafío que implica la modelización de la mesoescala, llegando a resolución horizontal de unos 100 metros.
Bibliografía
- Dynamics of limited-area models: Formulation and numerical methods. F. Mesinger, Meteorology and Atmospheric Physics Vol. 63.,1997.
- https://cpb-us-w2.wpmucdn.com/sites.uwm.edu/dist/8/663/files/2019/10/09-LBCs.pdf